548
簡單 MLP 架構示範
在說它的演算法機制與複雜公式前,我先用幾張簡單的圖說明流程。
訓練監督式神經網路演算法的流程,就像給機器人寫無數個有正確解答的題目。
藉由無數次的訓練,答錯修正權重,答對保持全重設置,讓神經網路判斷越來越準確。
圖解神經網路運作流程
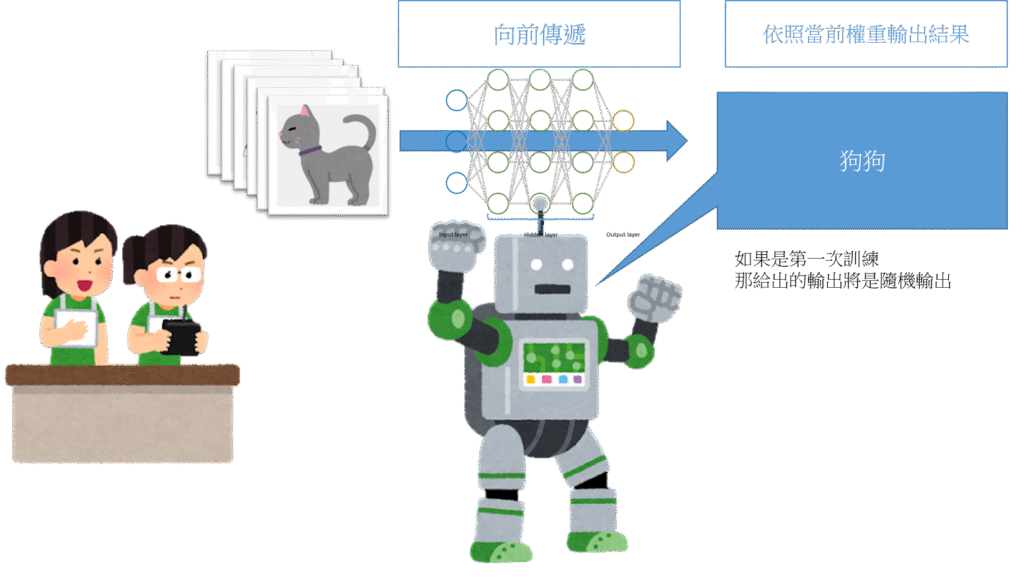
向前傳遞階段

我們將神經網路設置隨機的權重。
在第一次訓練時,將資料匯入,它會依照隨機的權重給予一個答案。
但因為判斷機制都是隨機的,所以答案也是沒意義的。
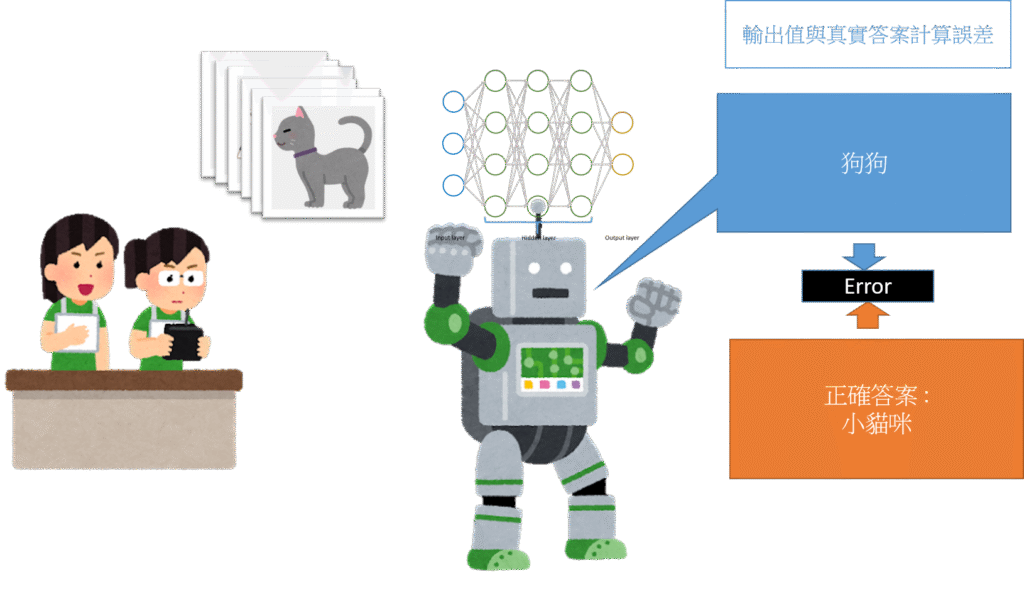
計算誤差值

計算誤差值,其實就是計算輸出值與真實值的距離。
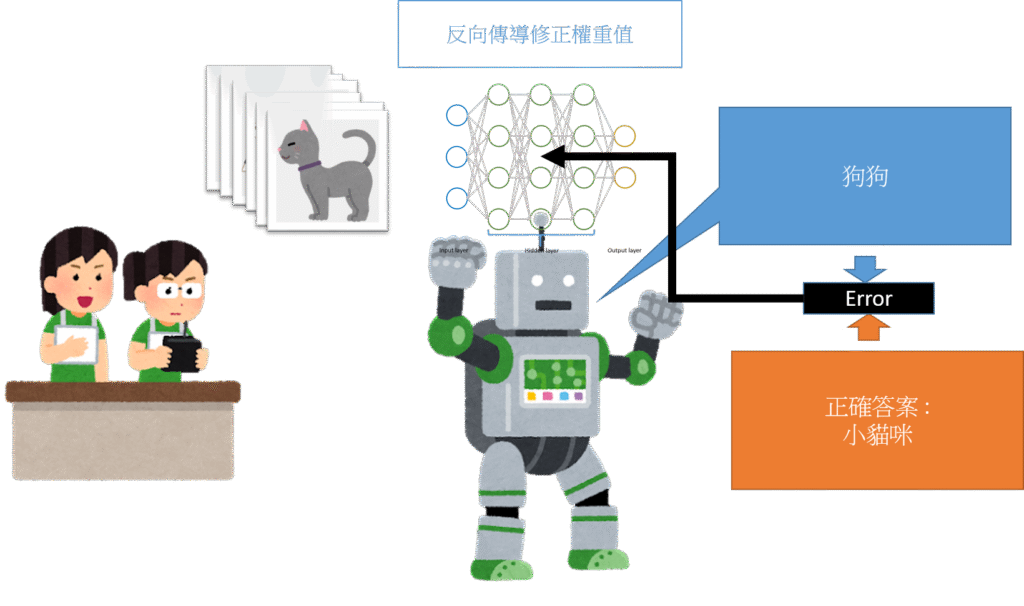
反向傳導修正權重

誤差越大,修正權重的力道就越大。
以此為一個循環,當神經網路經歷過無數個類似的問題後,對問題的精準度與包容度就會越來越高,誤差也就越來越小。
神經網路的學習規則
學習規則是由如何定義模型好壞,以及如何修正權重兩個方向討論,此階段討論參考引用 Matt Mazur 的文章推導。
在監督式學習神經網路當中,我們同時匯入有標籤的輸入值與真實輸出值。
再輸入值匯入模型後,模型經過計算產生出預測輸出值。
如何定義模型好壞,便是討論如何有效的計算預測輸出值與真實輸出值的差距,而定義出損失函數。
定義出損失函數後,每次匯入輸入值後,損失函數便會計算出此模型的誤差值,再藉有梯度下降法修正權重讓模型一步一步地使損失函數下降。
於是在整個神經網路就有兩個階段工作,第一階段為訊號向前傳遞並第二階段計算誤差、第三階段為反向傳導修正權重值。
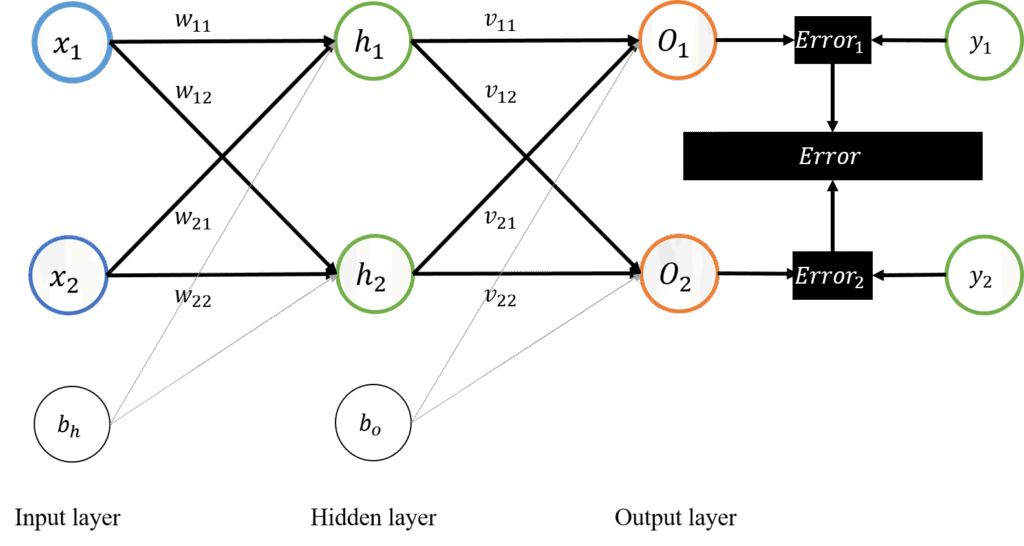
一個完整的神經網路模型,可能有多層結構,以簡單的僅有一層隱藏層且輸入輸出隱藏層皆只有兩個神經元的簡單架構做為神經網路計算範例,如下圖,並且依單一訓練資料匯入演示神經網路計算與修正的數學流程。

Jyajyun完整的AI學習文件目錄
- 最小單元神經網路結構 – 感知器,PERCEPTRON
- 激發函數(ACTIVATION FUNCTION)的可視化與理解
- 神經網路的經典架構 – 多層感知器 MLP
- 神經網路的學習規則
- 神經網路 向前傳遞 公式推導
- 神經網路 計算誤差值 公式推導
- 如何理解神經網路裡的梯度下降

