以類神經網路分析
隨機 GRY 時間序列模型
Analysis of the stochastic GRY time series model
using artificial neural networks
指導教授
陳企寧
研究生
呂諺嘉
摘要
股票交易是無數場資訊的博弈,這些買賣的交錯影響排列出一長串股價時間序列。
其中包含了大量的隨機性,但也蘊藏了可能提高投資報酬的模式。
我們以經濟物理的經典模型-"隨機漫步模型"為假設基礎
創造了一系列時間序列模型 - GRY 模型
一個產生綠球、紅球與黃球排列的時間序列模型。
設定排列模式規則外,並加上隨機規則,讓整體時間序列具有隨機性。
將 GRY 模型序列匯入不同的神經網路,驗證分析不同神經網路區分隨機與非隨機資料的能力與方法。
股票市場演化的數據科學
從大航海時期,荷蘭人在阿姆斯特河橋上買賣荷屬東印度公司的第一張股票時
便將猶如博弈的股票市場開啟了第一注擲骰。
時至今日投資人面對股市能不像以往豪賭般地的投注,而是由更多的數據判斷每次投資的價值。
從而衍生數據驅動決策 ,其基礎為處理資料結構分析,將其結果提供投資者決策的輔助。
然而面對複雜且多變量的數據指標,如何有效地選出合適的決策輔助也變得更加關鍵。
市場的高度隨機性與規則變遷 - 隨機漫步假說
倘若真實股票市場資料隨機性高達九成以上的問題且報酬率分布似正態分布,將導致整體報酬看似呈現隨機漫步。
物理學上的布朗運動的特性對於我們所認知的股票市場擁有相符的特性
所以在金融分析上布朗運動隨機漫步是進行市場討論時常引入的概念。
神經網路在金融市場時間序列的可行性
神經網路的特性是依照過往資料訓練,在高度複雜的問題裡,藉由複雜的結構,從中訓練出能讓訓練資料錯誤率自主逐步降低的一個經典演算法。
在學術與生活應用中,我們大量得使用這套演算法,這套演算法主要是用強擬合的方式,去降低誤差,如果訓練數據裡具有確切的規則,那這套算法幾乎能有效破解。
但因為複雜結構的關係,人類對於神經網路為何能夠這樣分類仍有許多未解之謎,許多人會稱之為黑盒子,因為複雜的結構讓科學家們缺少分析得可解釋性,僅能確定神經網路能藉由複雜的結構訓練出能分析資訊裡幽微的訊號。
為何要使用神經網路演算法 ?
結構複雜
複雜的結構讓神經網路有許多特點,也是這演算法一切的基礎,高度擬合複雜問題、自主學習能力變強、面對高度隨機問題也能找出背後的規則。
抗噪能力強
因其複雜結構關係,計算過程中有無數的神經元與權重能進行調整,即便某處的結構被隨機數據給破壞,整體的結構仍然能保持出色的計算能力。

自主學習能力強
受益於複雜結構關係,神經網路的自主學習能力很強,如果問題中確實有確定規則,同時數據量足夠龐大,神經網路通常都能有效地學習規則。
能因應需求調整結構
能夠調整結構的神經網路模型,讓計算時有更高的彈性。面對大型且複雜的問題,便能夠設計複雜會者變形的結構進行更有效地計算。
神經網路計算的結果 真的可信嗎?
儘管我們知道了神經網路強大的能力,但對其運作仍無法完全窺透,也無法有效地分析計算結果。
面對金融市場又是一場百年來的盲人摸象
即便在研究中真的應用神經網路分析金融市場
因沒有任何其他的理由佐證神經網路是真的學習到了股市的精髓
還是只是對過往有限的資料進行了高度的擬合。
而導致進行投資交易時,我們還是須面臨離大的風險。
問題背後的問題 - 神經網路能否適應高度隨機環境

神經網路的黑盒子特色
神經網路依照過往資料訓練,在高度複雜的問題裡,藉由複雜的結構從中訓練出能讓訓練資料錯誤率自主逐步降低的一個經典演算法。
因為複雜結構的關係,目前僅知道神經網路有強擬合的特性,但如何從中分析擬合過程與辦法,我們無從得知,所以許多學者稱它為黑盒子。

驗證神經網路在隨機問題裡的可行性
我們真正要確認的是,
神經網路是否能在高度的隨機裡找到隱含的規則。
以此為發想,我們可以設計一套模型。
設定簡單規則,其餘的內容都隨機,製造大量數據,讓神經網路訓練。
查看其訓練成果能否查找出我們設計的規則。
股市裡的隨機漫步
股票市場亦是如此,古今中外有許多學者與投資者在股票市場的殿堂外,藉由有限的資訊以管窺天試圖臨摹股票市場內是否真有一條優美的式子整合著整個市場的脈絡,抑或市場真的僅是瘋狂的人心混亂隨機漫步。
時間序列仿股票 GRY 模型
本篇由研究設計了一系列的模型-GRY 模型
以模仿真實股票市場時間序列的方式,設下規則與隨機度,做出多種不同的時間序列
其中序列包含三種元素-綠球、紅球與黃球,分別對應真實市場中的跌價、漲價與極小波動的漲跌。
應用神經網路分析,探討神經網路是否能對本研究的 GRY 模型中,破解我們為其設計的規則。
GRY 模型的設計,擁有高度的隨機性,讓整體回報看似隨機漫步,同時包含了我們設計的規則。
我們從中觀察神經網路對於這樣的狀態是如何一步步地自主訓練
探討在面對這些問題時遇到的情況,讓我們在真實股票市場中也有借鏡討論的機會。
GRY 模型設計規則
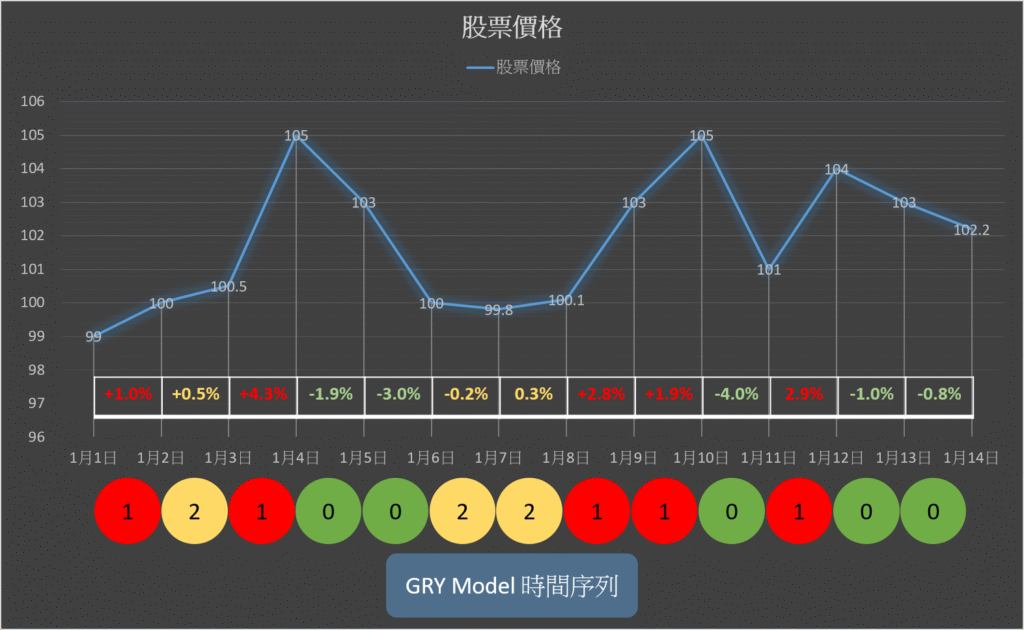
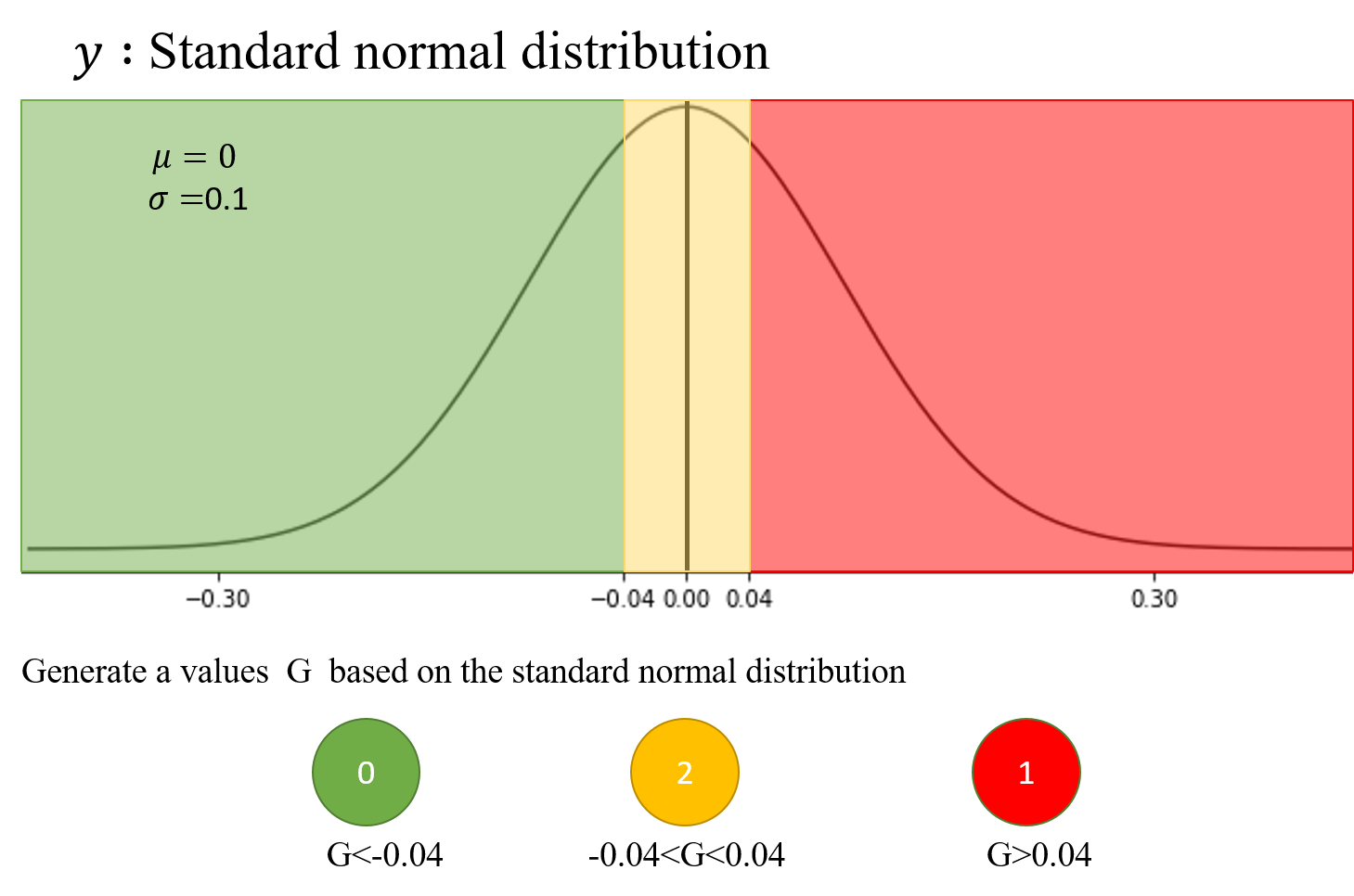
如上圖,本研究將每日的報酬率,轉化成另一種由紅球、綠球、黃球構成的時間序列。
將報酬率大於 0.6%的值視為紅球,報酬率介於 0.6% 到-0.6% 的值視為黃球,將報酬率小於 0.6% 的值視為綠球。
為何以 0.6% 為參考標準,因為股票市場買賣中有一個交易成本價,在 短線操作中買進賣出後交易成本價大約等於股價的 0.6%。
於是,複雜的股票漲跌變成了猜紅綠黃球的實驗。
本研究將進行一連串的假設以及測試,評測在不同的隨機度中,能否有效地掌握出正確的規則。
第一個假設 - 今日股價的報酬率,只會受前兩天波動影響
我們進行第一個假設,假設股市中含有以下規則,而後所有的發展趨勢都是建立在此之下的
規則一
今日股價報酬率
只會受到前兩天報酬率波動影響
規則二
前兩天若漲幅都大於0.6%
今日將反跌大於-0.6%的幅度
規則三
前兩天若跌幅都大於0.6%
今日將反漲大於0.6%的幅度
規則四
前兩日,一日跌幅大於0.6%
另一日漲幅大於0.6%
今日報酬率介於-0.6%~0.6%
規則五
若沒有以上幾種漲跌情況
今日將是隨機狀態
二對一 GRY Model 模擬問題
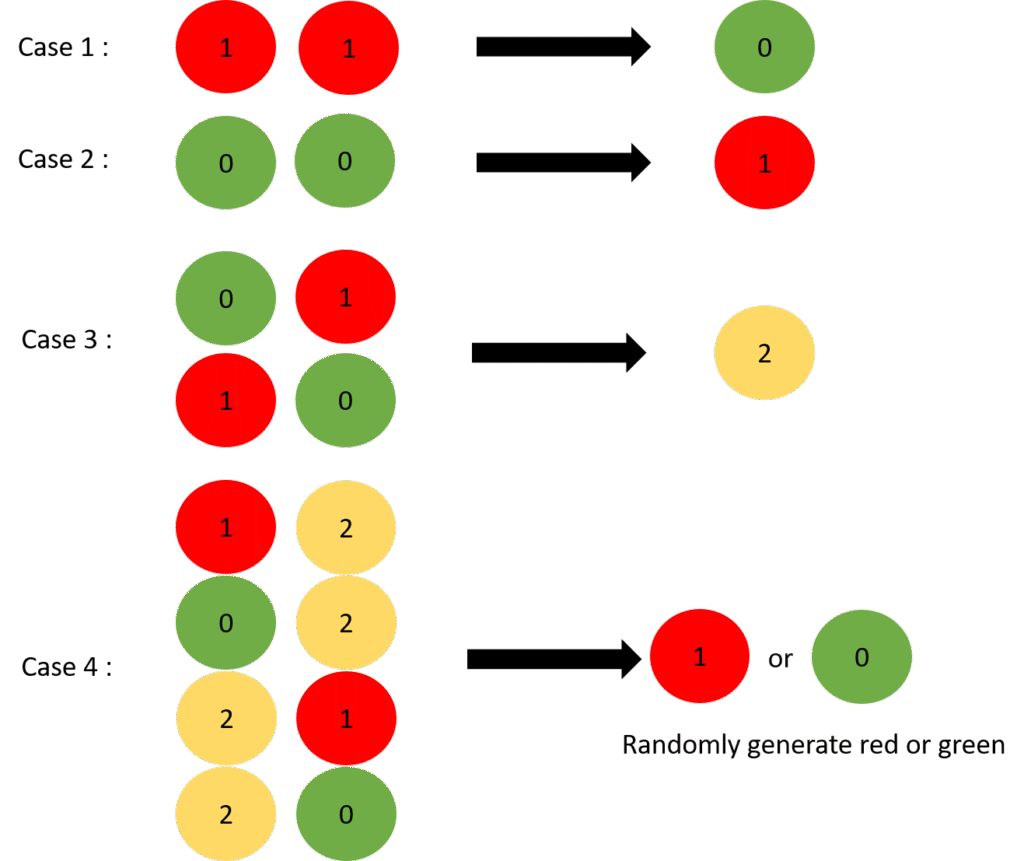
第一步 : 隨機產生兩顆任意顏色的球
第二步 : 從第三顆球開始,每次產生的球都會依照前面兩個顆球的顏色規則 產生不同顏色。
- 紅球+紅球 -> 綠球
- 綠球+綠球 -> 紅球
- 紅球+綠球 -> 黃球
- 綠球+紅球 -> 黃球
- 其他 -> 隨機
以此無限往下產生新的球,排列成一個長時間序列,我們生成了一個隨機程度為50%,長度為10000的時間序列,如下圖。

二對一 GRY Model 神經網路訓練
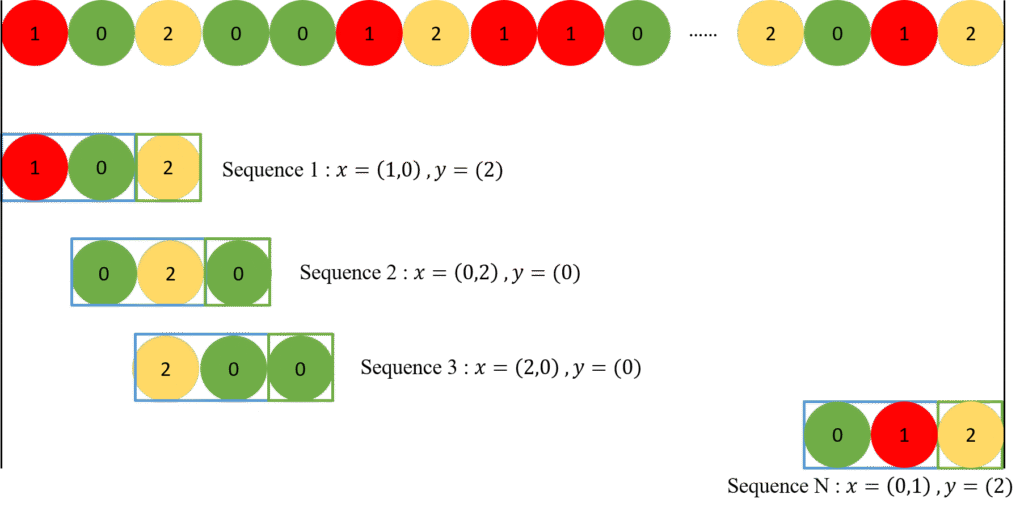
訓練資料準備
需要將長時間的序列切成一段段的小破碎時間序列當作𝑥,破碎序列的下一個 點即當作𝑦,切完一組,整體往後一顆球繼續下切。
此處小破碎時間序列𝑥的標籤長度為 2,𝑦的標籤長度為1,具體切法如左圖。
將切好的 998 筆𝑥與𝑦,分為兩個部分,前 800 筆當作為訓練資料、後 198 筆測 試資料,在訓練好模型後使用檢測模型的好壞。
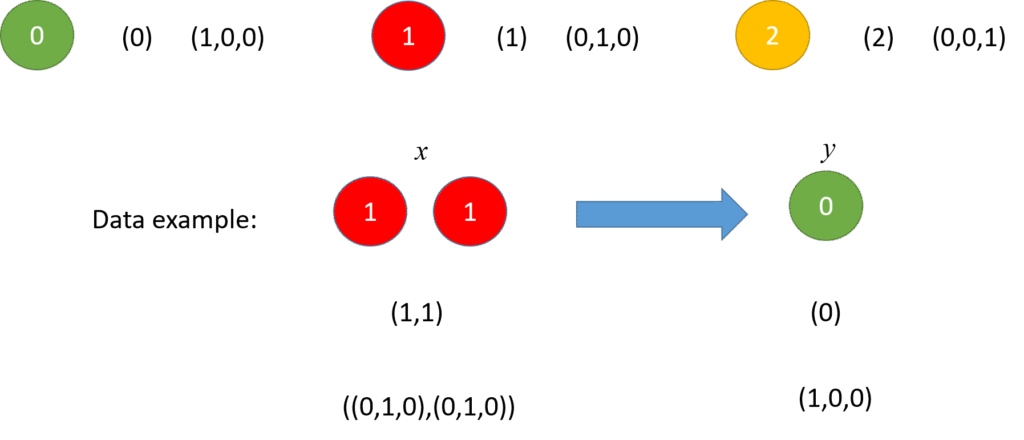
One-hot coding 轉換
將𝑥與𝑦進行 one-hot Coding 的轉換,讓原本的 0、1、2 數位訊號轉化為[1,0,0]、 [0,1,0]、[0,0,1]的三維數位訊號。所以原本的𝑥的長度(2)變成(2,3)、𝑦也從原本的長 度(1)變為(1,3),如下圖。而因為 MLP 架構下,多個維度的特徵必須轉為一個維度, 所以將原本𝑥的長度 (2,3)轉為一個維度的(6),y 的長度 (1,3)轉為一個維度的(3)
訓練神經網路的架構
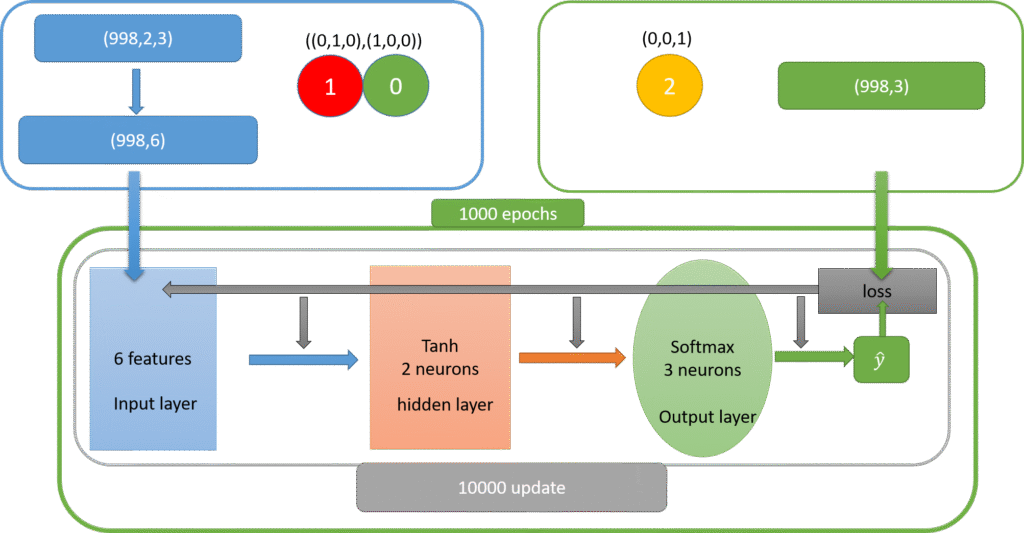
GRY Model 可視化介紹

GRY model 可視化特色介紹
我們的資料結構結果為一個三個維度的資料,所以我們能將結果可視化到一個 3D 的箱子中。
匯入資料進神經網路中,神經網路的輸出,一個三維的資料,我們能將此資料畫到 3D 箱子中如左圖。
同時因為最後的激發函數為 softmax,那會讓所有的輸出值總和等於 1,以此𝑦輸出值僅會在三角形的平面上。
可視化座標範例
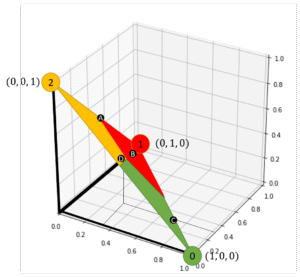
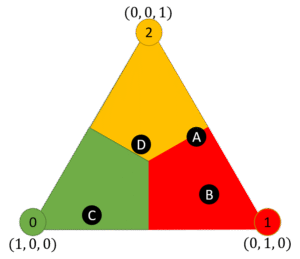

輸出數據的真實意義
我們設計的模型,輸出結果是一個三維座標,可用一個三維空間座標系標註。
而這三維數字背後真正的意義,其實是黃綠紅球的機率,轉化到真實世界為漲跌幅的機率。
越靠近角落,代表對某種預測的信心程度越高。
三頂點則是信心程度100%。
上述的A、B、C、D點,各有各自能解度的意義。
A點,預測為紅球,賺錢 : 跌幅>6%的機率為 2% ; 漲幅>6%的機率為 51% ; 漲跌幅在6%以內的機率為 47%
B點,預測為紅球,賺錢 : 跌幅>6%的機率為 18% ; 漲幅>6%的機率為 74% ; 漲跌幅在6%以內的機率為 18%
C點,預測為綠球,賠錢 : 跌幅>6%的機率為 72% ; 漲幅>6%的機率為 22% ; 漲跌幅在6%以內的機率為 6%
D點,預測為紅球,賺錢 : 跌幅>6%的機率為 34% ; 漲幅>6%的機率為 30% ; 漲跌幅在6%以內的機率為 36%
由A、B兩點我們得知,雖然預測結果都為賺錢,但其實A點的有點猶疑不定,B點的信心程度較高,但同時擁有較高的賠錢風險。
神經網路結果分析
如何算是神經網路克服了我們設計的 二對一 GRY model 的隨機問題 ?
如我們設定規則時講的那樣。
當輸入值有我們設定的正確答案時,輸出值需為正解,同時信心程度必須接近100%
當輸入值答案是隨機時,輸出只能答紅跟綠,同時紅跟綠信心程度必須50%左右,黃球信心程度需要接近0%。
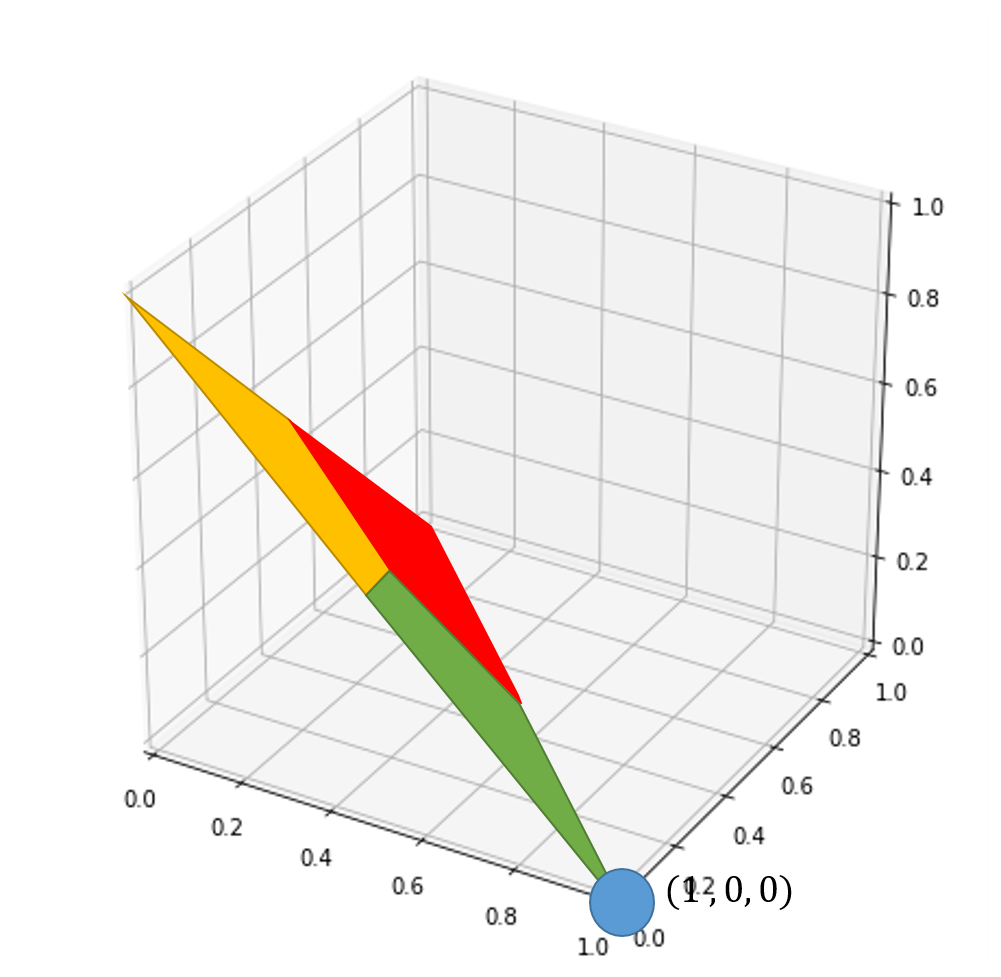
當輸入值是兩個紅球時
我們希望輸出結果必須判斷出綠球
同時需要接近100%的信心程度
可視化上需要再座標(1,0,0)附近
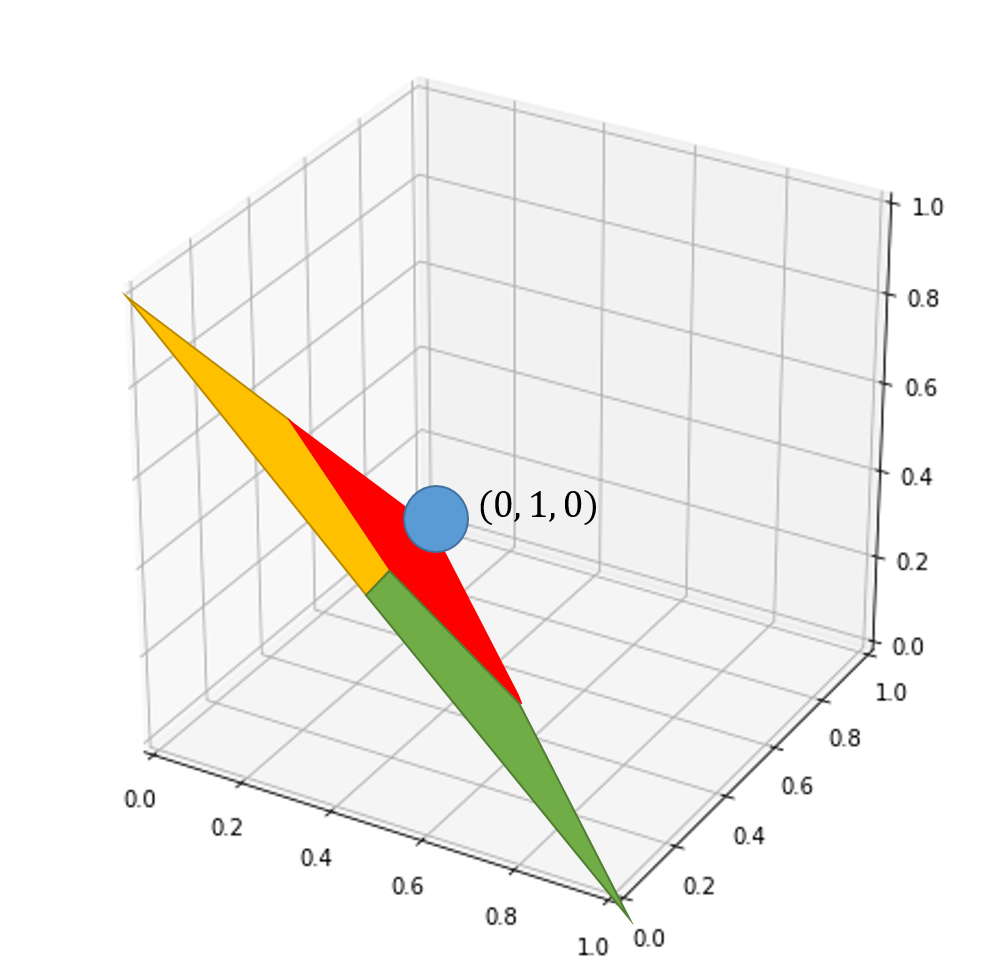
當輸入值是兩個綠球時
我們希望輸出結果必須判斷出紅球
同時需要接近100%的信心程度
可視化上需要再座標(0,1,0)附近
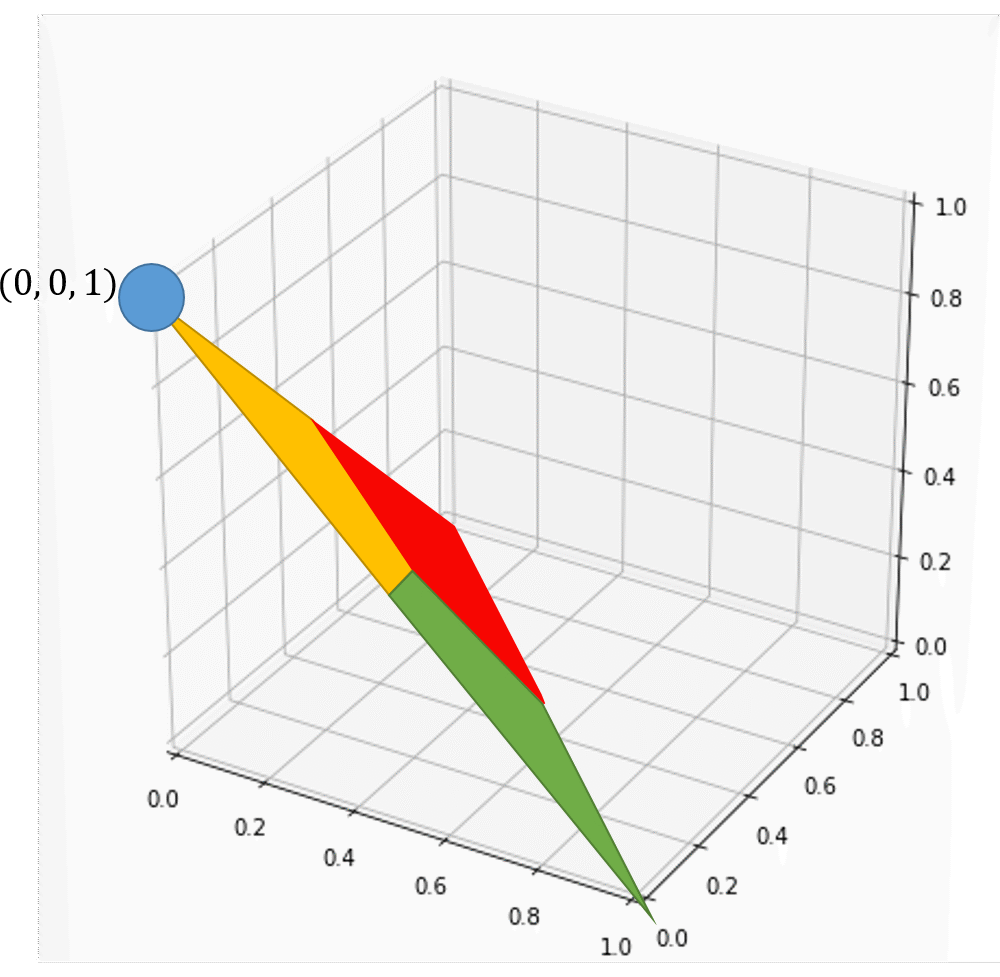
當輸入值x是紅綠或綠紅相間
我們希望輸出結果必須判斷出黃球
同時需要接近100%的信心程度
可視化上需要再座標(0,0,1)附近
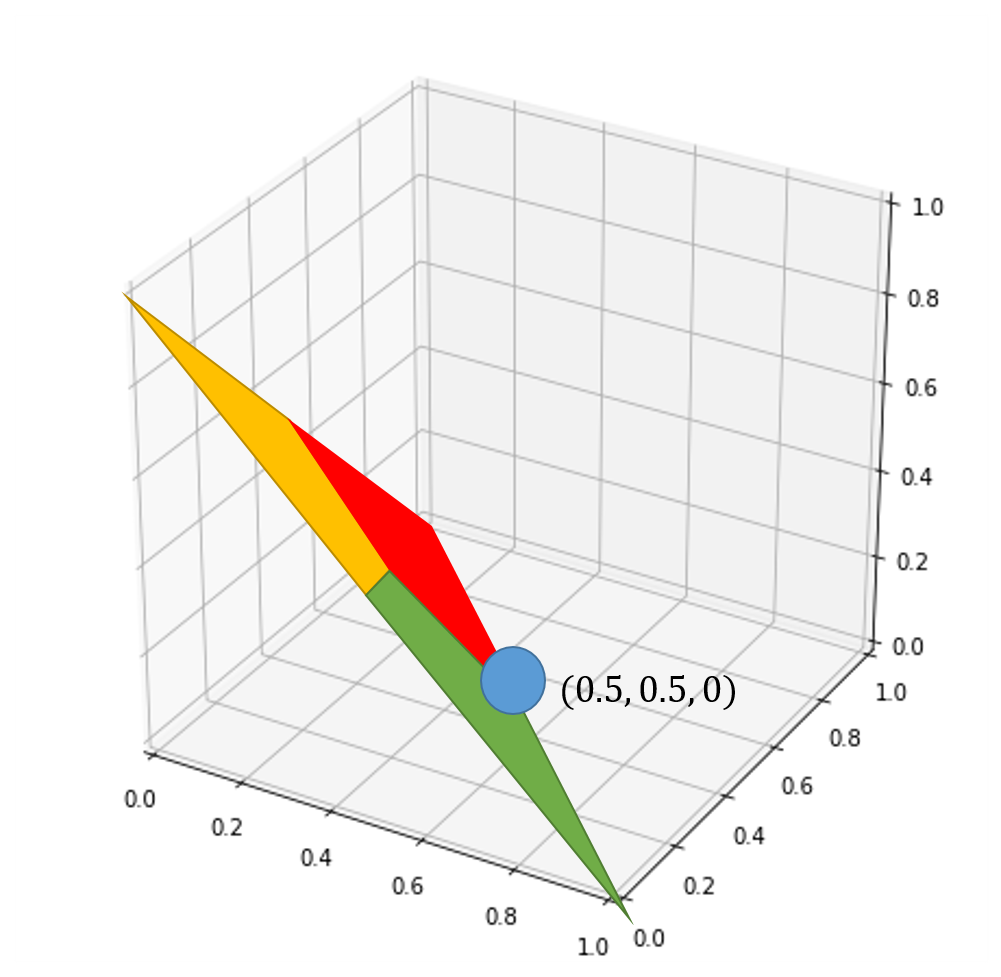
當輸入值是其他情況時
輸出值,只能答出紅跟綠。
同時紅跟綠信心程度必須50%左右,
黃球的信心程度需要接近0%
神經網路訓練過程
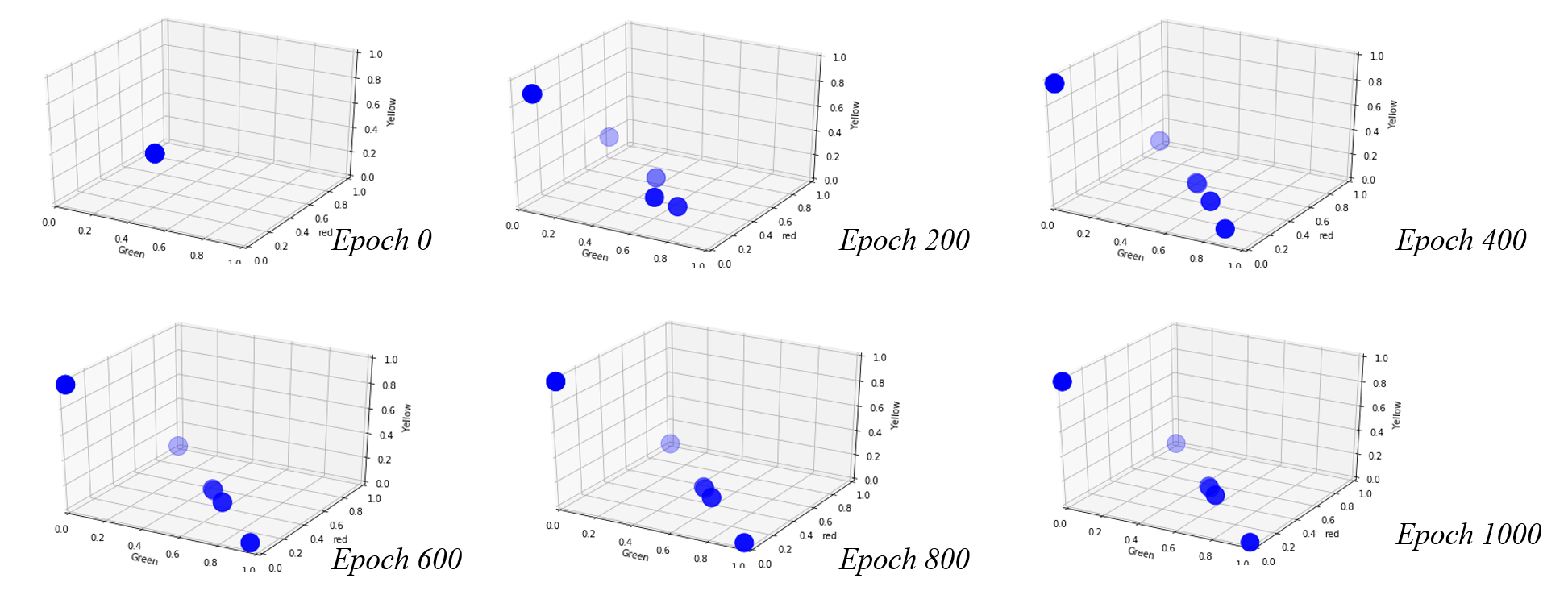
起初,所有輸出都聚集在某一個點,其原因為激發函數 softmax 的因素,因為 所有輸入資料特徵類似再加上權重是正態分布的給予,所以輸出層的結果數值會 差不多,經過激發函數,會將三個維度的資料呈現大約(1/3,1/3,1/3)的結果。隨著跌 帶次數的增加,有些點慢慢地被分開了,而有些點還在中間,在後期的訓練可以發 先整體有些點已經被分開到周圍,有些還遺留在中間。將最後一個 epoch 的分布圖 討論。分別查看那些匯入值𝑥會到角落、哪些會在中間徘徊。
成功驗證神經網路能有效破解第一個假設
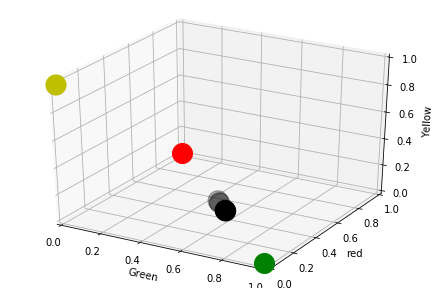
神經網路完美達到預期理想 - 破解隨機度50% GRY Model
再次將不同的資料匯入,同時在球體上標註其輸出值正確答案的顏色,其中黑色的代表實際值是隨機沒有規則的。
從結果來看發現,三個角落的顏色完全正確,同時那些隨機的數據也被擊中到了紅綠連線的中心點約一半的位置,完全達到設計實驗的理想值。
從這便能看出神經網路對於簡單的隨機問題有非常精準的判斷能力。
論文裡其他假設與GRY模型
在網路上僅簡短介紹了最簡單的GRY模型與神經網路驗證,但因為排列組合少,判斷資料短,隨機度低,所以其實很容易破解規則。
在論文裡收錄了更多更加複雜的模型與討論,其中包含以隨機漫步為基礎設計隨機度高達98%的模型,以及真實市場裡神經網路的驗證。
如有興趣歡迎引用、參考或者來信討論。
隨機漫步 98% 隨機度,GRY長序列模型
以經典理論隨機漫步設計
98%隨機程度,長時間序列10對1
探討真實隨機漫步下,神經網路的成效
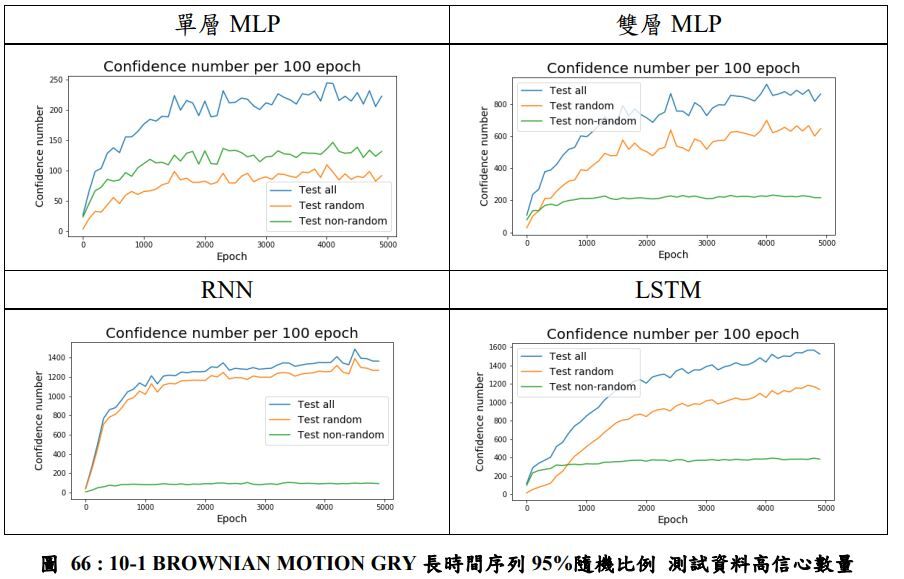
MLP、RNN、LSTM神經網路比較
經典神經網路模型除了最基礎的MLP外
還有以時間序列特色而設計且廣泛應用的RNN
以及LSTM,測試多種神經網路在高隨機下的成效

0050、2330 股票測試分析
以真實股價回測
標的為0050 與 2330 股票
測試理論世界中與真實環境中的測試差異
聯絡我們
Analysis of the stochastic GRY time series model using artificial neural networks
指導教授 : 陳企寧
研究生 : 呂諺嘉
呂諺嘉
電子信箱 : yenchialu@gmail.com
