在上一階段 MLP 討論到每一層神經元資料輸出到下一層之前都會經過不同形式的激發函數。
而接下來討論的是不同於傳統的全或無激發態。
取而代之的是一個非線性的數學轉換,增加了激發函數的複雜度使之也能模擬較複雜的非線性問題。
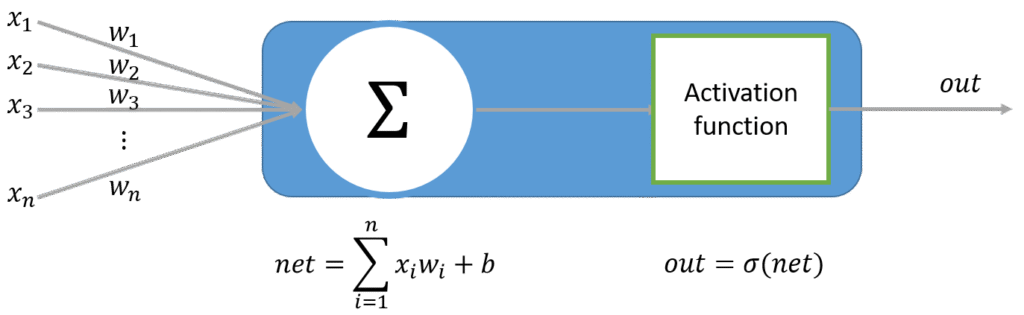
為何需要激發函數 ?
最主要目的是為了讓函數變成非線性因素
如果只是將無數個perceptron無數疊加,再深再大的神經網路也只是線性組合,無法做出有意義的映射關係。
依舊只能進行基本的線性可分問題。
這是神經網路最關鍵的一環,讓神經網路能解決更加複雜且抽象的問題。
Sigmoid激發函數
\sigma(x) = \frac{1}{1+e^{-x}}
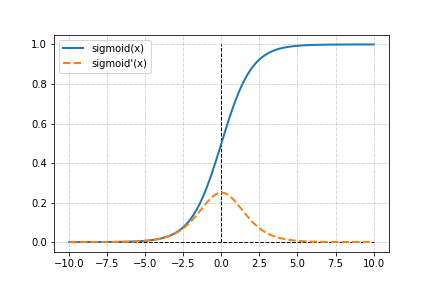
Sigmoid 激發函數,不同於傳統的全或無激發態,是一個平滑的曲線。
整個函數經過激發過程後也是微分可導狀態,有助於修正權重時梯度下降的計算。
在輸入值𝑥為極大或極小值時,Sigmiod 激發函數能夠將其壓縮至-1 或 1,不會讓過多
的極值影響整個結構的學習狀況。
其缺點為導數值較小,在之後的梯度下降法容易遇到梯度消失狀況。
如上圖,導數最高不到 0.4,且可反應區介於-5 到 5 之間,超過這個區間的輸入值,輸出值
會趨近於 1 或 0,並且梯度修正值趨近於 0 呈現梯度消失狀況,即無法修正。
Tanh激發函數
Tanh 是一個雙曲正切函數。
其樣貌和特色與 sigmoid 函數的曲線相對相似。
\sigma(x) = \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}
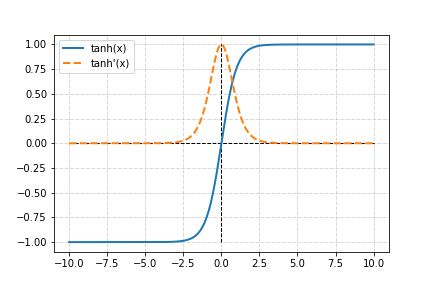
Tanh 的輸出是介於-1 到+1 之間,以零為中心的輸出在多層結構上可以更有效的收斂。
同時斜率變化也比sigmoid更加陡峭。
繼承 Sigmoid 所有優點,同時優化了整體的表現,但最主要的缺點並沒有得到改善,梯度消失的問題仍然存在。
Relu激發函數
ReLU 激發函數的輸出,在小於 0 的部分皆為 0,大於 0 的部分為線性。
\sigma(x)= max(0,x)
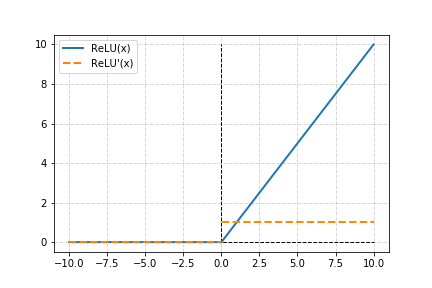
這樣的激發函數解決了 Sigmoid 與 Tanh 的梯度消失問題,便於建立複雜的神經網路模型。
也因為簡單的算式,大幅減少了計算的資源,速度會快上很多。
但隨之而來的是倘若修正速率設定步伐過大,很容易在訓練時讓許多的神經元死亡,一旦神經元死亡會削弱後面訓練時神經網路模型的複雜度,導致可能花費大量的運算,但真正在操作的神經元並沒有那麼多。
Softmax
\sigma(x)=\frac{e^{x_{j}}}{\sum_{k=1}^{k}e^{x_{k}}}\; for\; j=1,2,…,k
Softmax 激發函數,在處裡分類問題時 Softmax 激發函數的輸出彼此的特徵差異拉大,同時也會將較小機率的值保留,同時達到有效的分割空間,同時也保留細節,使其有更好的學習效果。
常用於分類問題的輸出層使用。
關於激發函數的推薦文章
- 深度學習筆記——常用的激活(激勵)函數 by CodingNote.cc
- 常見激活函數的介紹和總結 by CodingNote.cc
- 深度學習:使用激勵函數的目的、如何選擇激勵函數 by Mr. Opengate
- 深度學習領域最常用的10個激活函數,一文詳解數學原理及優缺點 by Sukanya Bag
Jyajyun完整的AI學習文件目錄
- 最小單元神經網路結構 – 感知器,PERCEPTRON
- 激發函數(ACTIVATION FUNCTION)的可視化與理解
- 神經網路的經典架構 – 多層感知器 MLP
- 神經網路的學習規則
- 神經網路 向前傳遞 公式推導
- 神經網路 計算誤差值 公式推導
- 如何理解神經網路裡的梯度下降

