如何理解神經網路裡的梯度下降

在計算誤差值後的下一階段，便是權重的修正階段。

權重修正的目的是在讓修正後，當資料再次匯入模型後的輸出結果與真實資料的差距更小。

藉由一步一步的修正，讓此差距逐步減小，也代表著讓誤差值逐步減小。

而修正權重的方式為梯度下降法。

其想法為模型會因為權重的不同而有不一樣的誤差值，在每一次匯入訓練資料候我們都能藉由誤差函數得到誤差值。

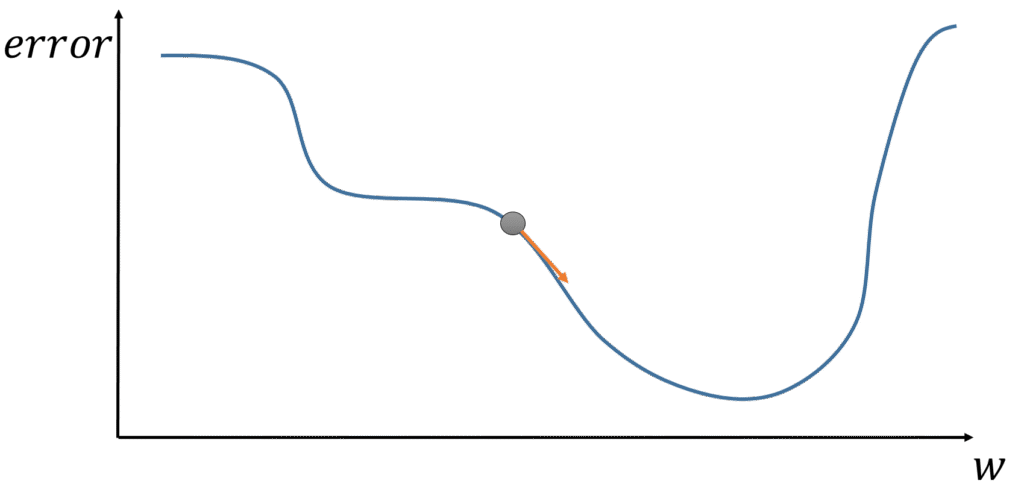
各個權重的調整對於誤差的改變如下圖 :

初始權重為圖上的灰色原點，在這點上計算出一個誤差值，下一步我們需要往誤差值更低的方向調整。

如圖，若向左方調整則誤差會變大，所以必須往右方調整。

模型如何知道要往右方調整，那便是用梯度下降法計算各個權重對於誤差的影響，而往誤差較小的方向調整權重。

具體方法是，計算各個權重對於誤差值的導數，便能計算出當下所有權重對於誤差值的梯度。

權重的修正便往梯度的反方向修正，就能往損失值較低的方向調整。

w_{new}=w_{old}-\gamma\frac{\partial Error}{\partial w_{old}}

其中 \gamma 為學習速率

Jyajyun完整的AI學習文件目錄

1. 最小單元神經網路結構 – 感知器，PERCEPTRON
2. 激發函數(ACTIVATION FUNCTION)的可視化與理解
3. 神經網路的經典架構 – 多層感知器 MLP
4. 神經網路的學習規則
5. 神經網路 向前傳遞 公式推導
6. 神經網路 計算誤差值 公式推導
7. 如何理解神經網路裡的梯度下降