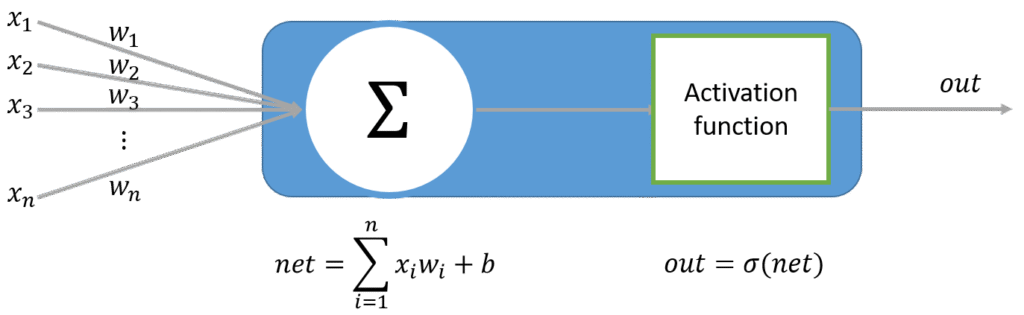
在說它的演算法機制與複雜公式前,我先用幾張簡單的圖說明流程。
訓練監督式神經網路演算法的流程,就像給機器人寫無數個有正確解答的題目。
藉由無數次的訓練,答錯修正權重,答對保持全重設置,讓神經網路判斷越來越準確。
圖解神經網路運作流程
向前傳遞階段
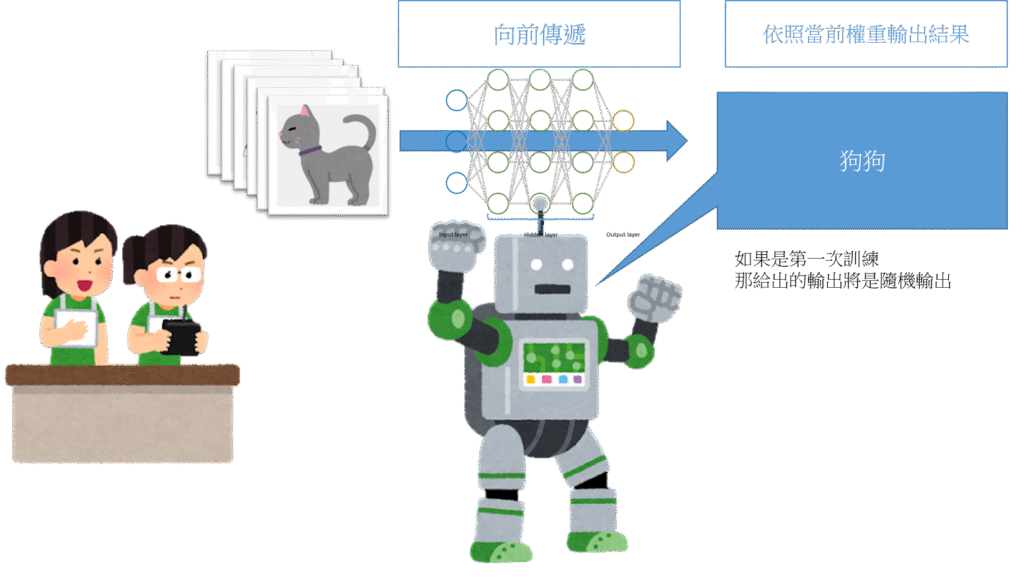
在說它的演算法機制與複雜公式前,我先用幾張簡單的圖說明流程。
訓練監督式神經網路演算法的流程,就像給機器人寫無數個有正確解答的題目。
藉由無數次的訓練,答錯修正權重,答對保持全重設置,讓神經網路判斷越來越準確。

在計算誤差值後的下一階段,便是權重的修正階段。
權重修正的目的是在讓修正後,當資料再次匯入模型後的輸出結果與真實資料的差距更小。
藉由一步一步的修正,讓此差距逐步減小,也代表著讓誤差值逐步減小。
而修正權重的方式為梯度下降法。
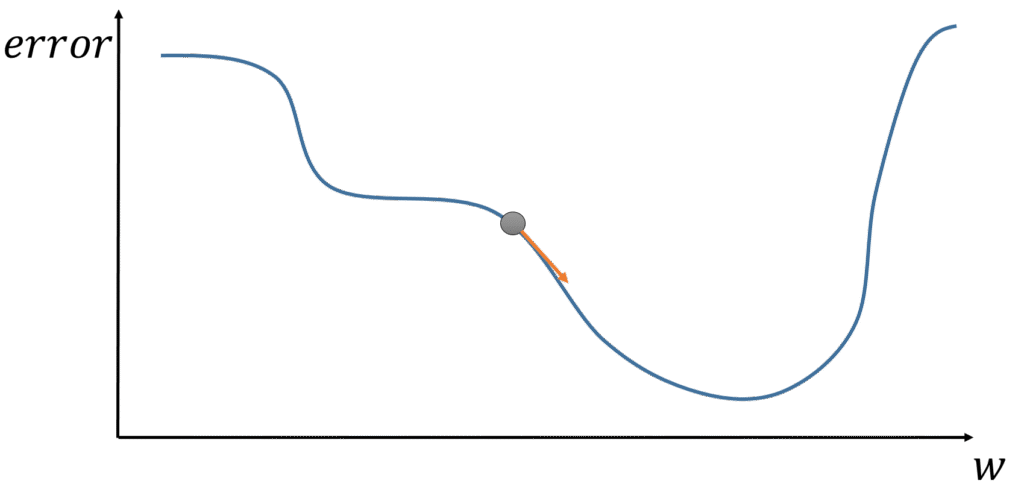
其想法為模型會因為權重的不同而有不一樣的誤差值,在每一次匯入訓練資料候我們都能藉由誤差函數得到誤差值。
各個權重的調整對於誤差的改變如下圖 :
方均根誤差(mean-square error、MSE)為神經網路裡常用的誤差函數之一,其公式如下
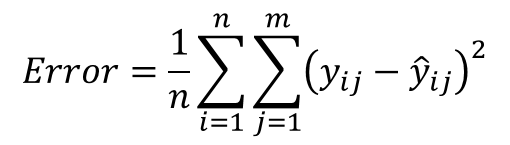
公式裡的𝑛為訓練資料總個數,𝑚為每筆資料𝑦的特徵數量,y_{ij}為真實值, \widehat{y}_{ij} 為模型預測值。在我們的示範算法裡,因為只有一筆訓練資料𝑛 = 1,每筆資料僅有兩個特徵𝑚 = 2,誤差值計算為
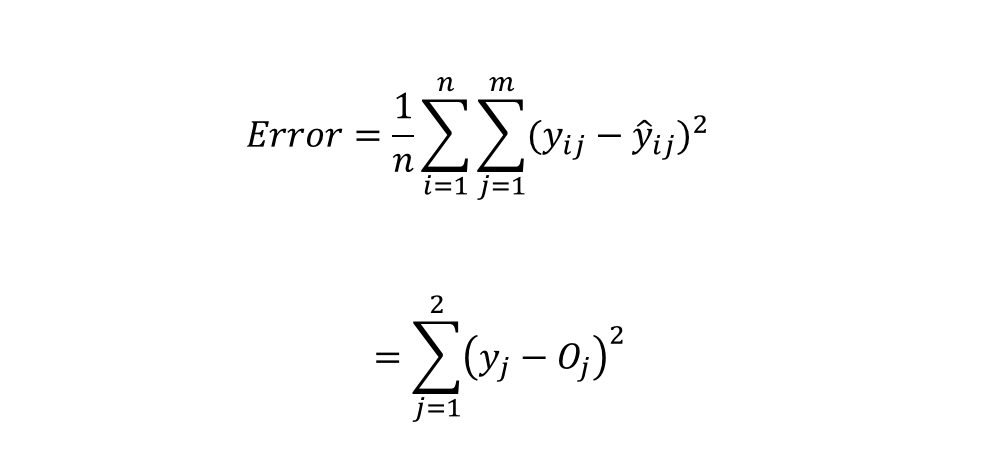
假設訓練的單一資料為 x=\binom{x_{1}}{x_{2}} 、 y=\binom{y_{1}}{y_{2}}
輸入層與隱藏層的權重與偏差值為w、b_{h} :
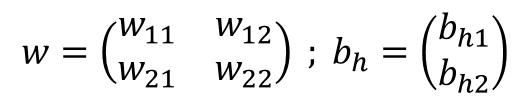
隱藏層與輸出層的權重與偏差值為 b、b_{0} :
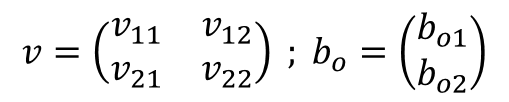
魔術方法的樣子,兩個底下線+方法名稱+兩底下線
__魔術方法 __
從應用上來看會發現,魔術方法與其他一般自定義方法的成效幾乎一樣,那為何還需要用這麼麻煩的方式命名?
此段說明參照
They’re mostly used for code that gets called implicitly when special syntax is used.
主要用於特殊語法時隱性調用的代碼
常用於以下場景
以及其他很多地方。
魔術函式別於一般自訂函數主要原因仍在於需要建立最初始的python必須做出最基礎的函式。
這些函式要能與上層C語言互動或者其他程式語言參照,同時也能與一般自定義函數做出最根本的區別。
所以絕大部分的魔術方法幾乎都是內建,除非程式需要動到整個python框架等級的操作,否則我們使用的魔術方法幾乎都是內置的,我們自定義的方法也不須參照魔術方法格式寫。
回傳物件的屬性名稱與值
#範例 1
#一個簡單的模組 Smartphone
#三個屬性 name,brand,price
#一個方法 on_sale
class Smartphone :
def __init__(self,name,brand,price) :
self.name = name
self.brand = brand
self.price = price
def on_sale(self,discount) :
self.price = self.price*(100-discount)/100
iphone_11 = Smartphone("iphone 11","Apple",1000)
iphone_11.on_sale(20)
print (Smartphone.__dict__) #返回所有可用的屬性(含內建與自定義屬性)
print (iphone_11.__dict__) #返回物件的自定義屬性
#執行結果
# >>> {‘__module__’: ‘__main__’,
‘__init__’:
‘on_sale’:
‘__dict__’:
‘__weakref__’:
‘__doc__’: None}
# >>> {‘name’: ‘iphone 11’, ‘brand’: ‘Apple’, ‘price’: 800.0}
回傳模組的路徑位置
#範例 2
import numpy as np
print(np.__file__)
print(np.ndarray.__file__)#執行結果
>>> 'C:\\Users\\Jia\\Anaconda3\\envs\\AI_L\\lib\\site-packages\\numpy\\__init__.py'
>>> AttributeError: type object 'numpy.ndarray' has no attribute '__file__'直接使用時,回傳主程式(當前程式)py檔名稱
當作屬性使用時,使用模組的py檔名稱
#範例 3
print(__name__)
print(np.__name__)
print(np.ndarray.__name__)#執行結果
>>> __main__
>>> numpy
>>> ndarray
「我不能太開心,否則得意忘形,會發生不好的事。」
告訴自己「別擔心,鎮定一點」,但卻更焦慮了,自己跟自己演起了靈魂分裂的對手戲。
你發現焦慮是不可控的,一旦嘗試控制,則會產生更多焦慮。
既然無法避免焦慮,也不能用意志力對抗焦慮,那我們有還有什麼方式能對抗呢 ?
演講全文 : How to cope with anxiety | Olivia Remes
關於講者 :
Olivia Remes 博士是劍橋大學的心理健康研究員、教練和勵志演說家。
Olivia 開發了一套應對策略,借鑒了多個學科並使用框架來為她的實踐提供信息和基礎,幫助人們獲得健康的心理,擺脫恐懼,以冷靜、堅定的心態面對挑戰、並於其中茁壯成長
她的著作在多國不斷再版,也持續推動與組織心理健康研討會以及主持一檔以心理健康為主題的廣播節目。
先從屬性(attribute)一詞描述,什麼是屬性,在python裡基本上在 . 之後的都是屬性。
所以取得某物件的屬性也可說是「從一個物件中取得附屬於該物件的另一個物件」,從屬性上也可以看出彼此的從屬關係。
以此理解,我們建立簡單的class。
#範例 1
class Smartphone :
main_purpose = "call up" #此為類別屬性
def __init__(self,year,price,brand) :
self.year = year #實例屬性
self.price = price #實例屬性
self.brand = brand #實例屬性許多文章中,會將上訴兩個名詞用不同的名字說明。
將變數與屬性就使用與理解上混為一談無傷大雅,但其實就技術層面與思維層面上不太一樣。
就python的文本裡即提到,在符號 . (dot)之後的即稱為屬性,並且屬性可以是唯獨或者可寫的。
但它是可寫時,我們便能賦值,這樣看起來便像一個變數,但因為他能表示出一個完整的從屬關係,所以以變數來形容他變得不太合適。
因為Perceptron結構的侷限,無法解決更複雜的問題。
既然一個無法解決,於是就將多個連在一起,總可以解決了吧。
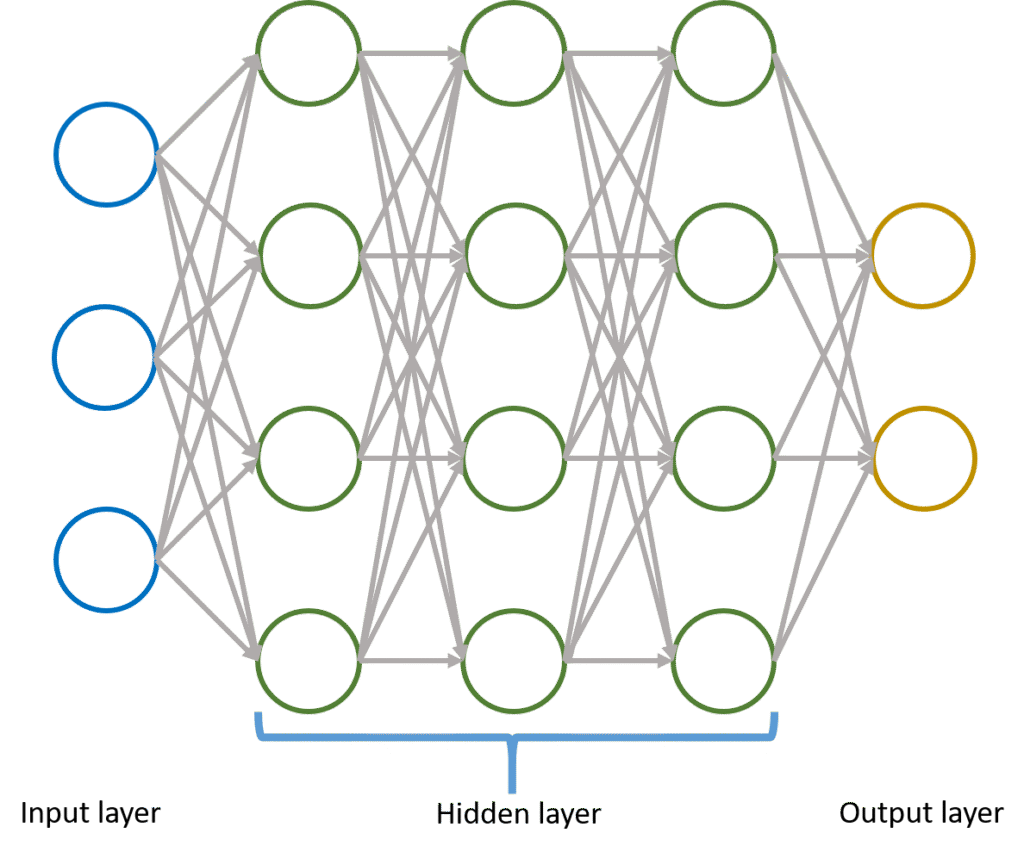
於是將無數個Perceptron連結,同時加上適當的激發函數,組成多層感知器Multilayer Perceptron(MLP)。
在資料傳遞上,單位神經元的輸出也可以變成下一層神經元的輸入,讓數據型態變得更高維,不斷的在向量空間映射。
可以同時融入更多參數集合的演算法,相比單元感知器,多層感知器面對更複雜的問題能進行更有效的模擬。
在物件導向技術中三個經常使用到的名詞,我們可以用很多的描述去側面形容他們的關係
#範例 1
#創建智慧型手機的類別,因為含有相機功能,所以繼承了相機的能力
class Camera :
def __init__(self,pixel) :
self.camera_function = True
self.camera_pixel = pixel
def take_picture(self) :
print ("喀擦,照片已存檔")
class Smartphone(Camera) :
def __init__(self,name,brand,price,pixel) :
super().__init__(pixel)
self.name = name
self.brand = brand
self.price = price
def on_sale(self,discount) :
self.price = self.price*(100-discount)/100
#創造一個物件,雖然沒給變數參考他,但他確實是個存在記憶體中的物件,也是smartphone的一個實例
Smartphone("iphone 11","Apple",1000,1000)
#又創造了一個物件 iphone_11,他是個物件,同時也是Smartphone的實例,同時也是Camera的一個實例
iphone_11 = Smartphone("iphone 11","Apple",1000,1000)
iphone_11.on_sale(20)類別很好區分,在上述範例可以理解,類別其實就是class裡的所有東西,是我們製作物件的一個藍圖,我們定義了一些屬型(name,brand,price),也定義了一個方法(on_sale)。讓之後有人要在做出Smartphone這種類型的物件時,能直接使用。
那物件跟類別怎麼區分呢,其實可以按照字面上的意思來形容。
從上面程式碼的例子,我有一台iphone 11,他除智慧型手機定義的東西,還繼承了相機的內容。
我們用isinstance(),判斷是否有繼承關係以及判斷iphone 11是否為Camera的一個實例。
print(isinstance(iphone_11,Camera),isinstance(iphone_11,Smartphone))#輸出結果
>>> True True
這個例子,我們有以下幾個正確的描述:
以幾以下幾個”錯誤”或者”不全”的描述
在上一階段 MLP 討論到每一層神經元資料輸出到下一層之前都會經過不同形式的激發函數。
而接下來討論的是不同於傳統的全或無激發態。
取而代之的是一個非線性的數學轉換,增加了激發函數的複雜度使之也能模擬較複雜的非線性問題。